QSNP Partners from DTU propose a set-up for a long-distance nonlocality test with entanglement swapping and displacement-based measurements
1 February 2024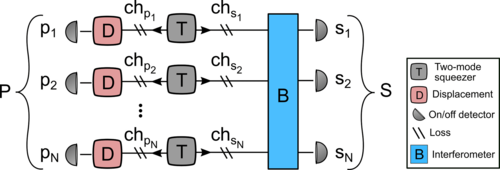
Researchers from the Center for Macroscopic Quantum States (bigQ) at the Technical University of Denmark, DTU, and partners of QSNP, have published a study in in which they analyze an all-optical setup which enables Bell-inequality violation over long distances by exploiting probabilistic entanglement swapping.
Bell inequalities, named after physicist John S. Bell, are a set of mathematical inequalities that suggest the presence of non-local correlations[1] between entangled particles. Experiments have provided strong evidence that the predictions of quantum mechanics are in odds with classical mechanics, which re-enforces the idea that local realism, or principle of locality, where things that change can only be affected by other forces that is local. However, achieving a robust and conclusive violation of Bell inequalities in experimental settings presents some challenges.
In this study, the researchers delve into the complexities of conducting Bell violation experiments in quantum mechanics. A Bell test is an experiment to decide whether the world is really as strange as quantum mechanics says it is, and whether Nature itself agrees with the principle of locality of Einstein or with Bohr’s conception that you the properties of an object are not defined until you observe it.
The main challenges of these experiments are the loopholes, that is, ways in which nature, or an eavesdropper, can arrange experimental outcomes so the experiment appears non-local while in reality it is not. The detection loophole arises because not all emitted particles are detected during the experiments mainly due to inefficient detectors. Even more, the locality loophole is present if measurements are performed such that a subliminal signal can transfer information between measurements stations during a measurement sequence. To address this loophole matter, scientists have developed high-efficiency detectors and have devised an experimental setup with spacelike separations, such as using distance entangled particles or space-like separated measurements on a single particle. These setups provide stronger evidence against local realism.
To overcome these challenges and push the boundaries of Bell violation experiments, in their study, the team proposed an experiment using quantum optics techniques and tools such as a two-mode squeezer, displacements and click detectors (on-off detectors). Two-mode squeezers are devices that generate entangled photon pairs. These squeezed states of light can enhance the precision of a measurement, due to techniques that help reduce the shot-noise produced by photons. Two-mode squeezer generate weakly squeezed two-mode squeezed vacuum states with half of each state sent a short distance to an on-off detector, and the other half sent to a distant interferometer.
For an experiment of these characteristics, the choice of measurement settings is a critical factor in determining whether non-local correlations are observed. To achieve a conclusive violation of Bell inequalities it is essential for the experiment to select measurement settings that ensure a strong correlation between the entangled particles. In the proposed experiment multiple parties are involved, each with an independent setting.
This paper explores strategies for optimizing Bell violation in the proposed experiment. One key finding is that there exists an optimal squeezing parameter that maximizes the Bell violation. The experiment robustness against dark counts is analyzed: at lower dark count rates, achieving a violation of the Bell inequality is more feasible, while it becomes more challenging at higher rates.
The proposed experiment leverages the precision of quantum optics tools and shows some promise in addressing the main challenges. A configuration with two-mode squeezers and high-efficiency detectors offer advanced capabilities for generating and measuring entangled photon pairs. While the impact of experimental imperfections cannot be underestimated, understanding the relations between them and their effects on the Bell inequality violations is crucial for interpreting experimental results accurately.
Tools for Quantum Optics
Quantum optics tools offer significant advantages. However, imperfections can still impact on the experimental results, some sources of imperfections are:
- Dark counts: dark counts refer to false counts in the detectors that occur even in the absence of incident photons. Experiment’s robustness against dark counts depends on the probabilities of it happening. If the dark count is too high it becomes challenging to obtain conclusive results. Advanced detector technologies can be used to mitigate dark counts.
- Channel loss: the transmission of entangled photons through optical channels can result in losses due to absorption and scattering. The analysis of the experiment shows that using more parties can make it easier to achieve non-locality even in the presence of channel loss. However, there is a critical transmission threshold beyond which the experiment’s robustness diminishes. This threshold represents a limitation based on the transmission distances.
- Phase and amplitude noise: phase and amplitude noise in optical components can introduce errors in the measurements, potentially reducing the strength of the Bell violations. There must be careful control to minimize the sources of noise to maintain the experiment’s accuracy.
Reference: Proposal for a long-distance nonlocality test with entanglement swapping and displacement-based measurements. Anders J. E. Bjerrum, Jonatan B. Brask, Jonas S. Neergaard-Nielsen, and Ulrik L. Andersen. Phys. Rev. A 107, 052611 – Published 23 May 2023.
[1] Nonlocal correlations are a quantum phenomenon that constitute a stronger form of correlations than quantum entanglement

Sketch of the analyzed setup with N parties. The left-going modes are labeled Pn, and the right-going modes are labeled Sn. A detector associated with a mode is given the same label as that mode. The measurement performed by the detectors in S effectively swaps the N bipartite entangled states, from the two-mode squeezers, into an N-mode entangled state. “ch” abbreviates channel.
